Ciaccona with Just Intonation:
A Practical Guide to Violin Tuning / A Wilderness Journey with Bach
Josh Modney
I entered the rehearsal room violin in tow, anxious to work with the staff pianist. The repertoire was a Beethoven sonata for violin and piano. Or maybe it was Brahms? The specifics are of little importance as this was a scenario that played out many times throughout my student years. We rehearsed the piece for forty-five minutes, maybe an hour. It sounded horrendous. I left the rehearsal feeling totally deflated. I had put in the time diligently practicing the music and had worked with my teacher on the nuances of the violin part, yet the first several rehearsals with piano always sounded grating and left me disoriented and unmoored. I knew the problem was likely related to tuning, but I didn’t know how to fix it except for a directionless feeling that I needed to practice more. Based on the information available to me as a student of the violin conservatory tradition, I could only conclude that I was a violinist with “bad intonation.”
After a few more rehearsals the tuning and blend would always get better, and I’d shrug it off and move on. I only realized many years later the root of the problem that created this cycle of demoralizing episodes. It was after grad school, and I was just starting out in the New York City contemporary music scene and loving every minute of it. I was playing with the Wet Ink Ensemble, co-founded a new-music string quartet (Mivos), was working with composers like Sam Pluta, Taylor Brook, Eric Wubbels, Kate Soper, and Alex Mincek, and taking any gig I could get. Making music in this community of adventurous artists provided the energy that led me to a serious investigation of tuning systems and, in particular as the system perhaps most applicable to string players, just intonation (JI). I read Harry Partch and Kyle Gann. I chatted with other tuning nerds. My mind was blown, and the shape of my artistic practice on the violin was radically changed for the better.
So, why did those student violin and piano rehearsals sound so ugly? Answer: because the modern piano is tuned in equal temperament (ET), and solo violinists do not play in ET. Indeed, it is virtually impossible for a string player (or a singer, or any human performing on a non-fixed-pitch instrument) to play in ET without a pitch reference like a keyboard or a digital tuner. The intervals of ET represent an averaging that is out of sync with the natural overtones of the harmonic series and are therefore very difficult to intuit by ear. The student dutifully practicing their sonata part alone is practicing tunings that sound vibrant and sonorous on solo violin, likely an intuitive mix of 5-limit JI, Pythagorean, and ET. The repetition of practice ingrains those intervals into muscle memory, and when overlaid onto the piano’s ET, almost every pitch is “out of tune” to varying degrees. If, as is the case with most students, you don’t know to expect this phenomenon, it is completely bewildering, and the tuning discrepancies leave an impression of not only clangorous pitch, but also an extremely off-putting harshness of timbre.
I place “out of tune” in quotes because it is a subjective and perhaps even misleading phrase. In the scenario above, it might be assumed that the violinist is playing “out of tune” by not agreeing with the piano’s pitch, when in reality the violinist and the pianist are each playing on their own grid with its own internal logic. It just so happens that the grids are incompatible in the context of the goals of classical music performance, and over the course of rehearsal the systems must be reconciled. In this case, the only possible reconciliation is for the violin to adapt to the piano’s fixed tuning system.
Needless to say, intonation is an extremely complex subject for string players. It’s one of the more difficult aspects of playing—there are many ways of approaching it—and as a result it comes with a good deal of emotional and psychological baggage. The established conservatory pedagogy of the past seventy years or so, which remains the prevailing method of teaching the violin, sets up a dichotomy of “in tune” and “out of tune” without ever really offering an explanation. I think this vaguery has to do with preserving a sort of mysticism around intonation, essentially a qualitative approach that allows a soloist or string quartet to make spontaneous decisions about tuning that, in the hands of masterful musicians, can be deeply affecting. But how does one achieve that mastery? There needs to be a quantitative side too, and, beyond the requisite fluency with the dominant system of ET, that side is sorely underrepresented in string pedagogy and even among professional performers. In my experience, fluency in systems beyond ET has been liberating, providing a collection of grids that can be mentally overlaid on the violin’s fingerboard, which, far from straightjacketing musical decisions, support creativity by training the ear to recognize ever finer gradations of pitch. JI has opened up a universe of harmonic, timbral, and expressive possibility on my instrument, provided a set of tools for measuring tuning accuracy using nothing more than the violin itself, and led me not only to fascinating collaborations with composers and an expanded language for improvisation, but also back to a new relationship with J.S. Bach’s towering Sonatas and Partitas for solo violin.
PART ONE: GRIDS
I. “INTUITIVE VIOLIN TEMPERAMENT” AND GENERAL PRINCIPLES: HARMONIC SERIES, LIMITS, COMMAS
There are countless tuning systems that might factor into a quantitative approach to violin intonation. The systems that I deal with primarily as a violinist are JI, Pythagorean (which is a subset of JI), and ET (including not only semitones but also smaller equal divisions of the octave like quarter and eighth-tones). In brief – just intonation is a broad term for tuning according to the ratios of the harmonic series. Pythagorean is a type of JI in which all pitches are derived from perfect fifths (that is to say, 3-limit JI). Equal temperament is a tuning in which the Pythagorean comma (the age-old keyboard tuner’s dilemma—the difference between 12 purely tuned fifths and 7 octaves, about 23.5 cents) is divided equally among all 12 semitones in the chromatic scale. For violinists, ET is important because it is the dominant system, and keyboards are tuned that way. Pythagorean is important because the violin strings are usually tuned in perfect fifths. JI is important because it makes the violin resonate the most sonorously. Whether consciously or not, the Western classical violinist is steeped in all of these systems, and in the absence of piano or another fixed-pitch instrument, violinists tend to play in a mashup of all three, something like “intuitive violin temperament.”
In practical terms as a violinist practicing and performing solo, the key to unlocking a self-verifying approach to intonation is in the cross-referencing of different levels of JI of increasing complexity: Pythagorean (3-limit), 5-limit, 7-limit, 11-limit, etc. Pythagorean is especially important since it employs only perfect fifths to derive all pitches, so it relates directly to the violin’s strings, which are most commonly tuned in perfect fifths. So in a sense, the violinist is practicing using their fingers to superimpose higher-level tuning grids (5-limit and above) onto the fixed grid of open strings (Pythagorean/3-limit).
To understand the concept of limits, we need to take a look at the harmonic series. The figure below shows the harmonic series of the violin G string up to the 13th partial (Fig. 1). The harmonic series is the infinite spectrum of overtones present in resonating bodies such as strings and columns of air. The partials of the harmonic series correspond to whole-number divisions of the resonating body. The fundamental (1st partial) is the strongest, the main sound that we hear. The relative strength of the other partials in an acoustic sound is a major factor in what we perceive as timbre (e.g., the difference in sound between a violin and a clarinet). String instruments provide a convenient visual guide to the harmonic series. The 2nd partial may be produced by lightly touching the string at the point (node) exactly halfway up the fingerboard, dividing the string in two parts. The 3rd partial is produced by touching either the node one-third up the fingerboard or the node two-thirds up the fingerboard—these are the two possible nodes that divide the string into three parts.

Fig. 1 – G string harmonic series
Working our way up the harmonic series, the 4th partial is the first number we encounter that is not a prime. There are three nodes along the violin string that produce the 4th partial, dividing the string into quarters (one-quarter, two-quarters, and three-quarters up the fingerboard). Here’s the key difference: two-quarters is reducible to one-half. By touching the string at the halfway point, you will only hear the 2nd partial. The 4th partial is there as a component of the sound, but the lower partial predominates. The same is true of any node along the string – what we are hearing is the lowest prime-number partial at that location. So, by touching halfway up the string, we hear the 2nd partial, but also the 4th, 6th, 8th, 10th, and all further factors of 2. By touching either of the 3rd partial nodes, we are also hearing the 6th, 9th, 12th, 15th, etc.
Prime number divisions of the string have strong identities, and are very important in the way that we perceive and group pitch relationships. The harmonic series provides the basis for constructing intervals and scales. The simplest scales that can be constructed based on these whole-number divisions of the string are Pythagorean scales, which derive pitches using the interval of the perfect fifth, the same as the ratio between the 2nd and 3rd partials of the harmonic series (3:2).
I find it helpful to look at the harmonic series (Fig. 1) to visualize how intervals and scales are constructed. (It certainly also helps to have a tactile relationship to these locations on the string as a violinist.) Pythagorean scales are “3-limit,” that is, the highest prime number that may be used to construct the scale is 3. So any multiple of 3, 2, or 1 is fair game. The key intervals involved here are 2:1 (the octave), 3:2 (the perfect fifth), and 4:3 (the perfect fourth, which is the inversion of a perfect fifth).
Here is a Pythagorean scale in G-Major, with the ratios used to derive the pitches (Fig. 2):

Fig. 2 – Pythagorean G-Major scale
All of the numbers used to construct the scale are divisible by 2 or 3. Some of the ratios are simple, like the 4:3 perfect fourth or the 9:8 major second. Others are complex, like the 81:64 Pythagorean major third. We perceive simple ratios as “consonant” and complex ratios as “dissonant.” The Pythagorean major third is widely regarded as unpleasant. For most music, the “sweet,” consonant sound of the 5:4 major third is preferable (5:4 is the ratio between the 4th and 5th partials of the harmonic series; see Fig. 1 above). But the 5:4 major third is not a possibility in the Pythagorean pitch family, since it involves a prime number higher than 3. In order for the 5:4 interval to exist in a tuning system, the system must be 5-limit or higher.
The incommensurability of primes is a dilemma when it comes to tuning fixed-pitch instruments. If you stack up 7 octaves (powers of 2) and 12 perfect fifths (powers of 3), you will arrive at a pitch that is about an eighth-tone shy of a unison. This discrepancy, about 23.5 cents, is known as the Pythagorean comma. Similar fissures open up between all of the prime number families. The Pythagorean comma represents the fissure between powers of 2 and powers of 3. The rift between powers of 3 and powers of 5 is encapsulated by the syntonic comma, which is the difference between the 81:64 Pythagorean major third and the 5:4 (5-limit) major third, about 21.5 cents. Next, the difference between the 16:9 Pythagorean minor seventh and the 7:4 (7-limit) minor seventh is called the septimal comma (27.25 cents). There is a comma for every rung that one ascends up the ladder of primes (the next two, which are also quite beautiful and useful, are the undecimal and tridecimal commas). These discrepancies are the reason for the advent of temperament—in order for a fixed-pitch instrument like a keyboard or guitar to perform music in different keys, compromise is a necessity. There is plenty of excellent literature on tuning and temperament that explores these intricacies. For starters, I recommend checking out Genesis of a Music by Harry Partch and How Equal Temperament Ruined Harmony (And Why You Should Care) by Ross W. Duffin. Suffice it to say, this ancient dilemma for keyboard tuners is a gift for string players, a universe of possibility at our fingertips.
II. THE EAR AS TUNER – BEATING AND DIFFERENCE TONES
Nature provides two wonderful tools for verifying intervals by ear—beating (an acoustic phenomenon) and difference tones (a psycho-acoustic phenomenon). The violin sits in a sweet spot of register that makes these tools particularly effective, so that you can find almost any interval involving primes up to the 17th partial or so with accuracy.
Beating is the acoustic interference between sound waves. When two pitches are played simultaneously in a simple ratio (e.g., 3:2 perfect fifth, or 5:4 major third), the sound is pure and placid. If the pitches are slightly out of tune (i.e., sounding as a very complex ratio), the upper partials of the two notes will interfere with each other, which manifests in our ears as beating. As one works with JI ratios of increasing complexity, beating becomes less useful as a guide for accurate intonation. For instance, an 11:8 dyad (the undecimal tritone) will have beating as a noticeable component of the sound even when played perfectly in tune, because of the acoustic properties of the violin. However, you can still hear a ratio like 11:8 “lock” into a characteristic timbre when it is correct. In the case of more complex ratios, you are essentially memorizing the sound of the beating pattern and the resultant timbre.
For me, difference tones are the most useful tool for verifying intervals by ear. Difference tones are a psycho-acoustic phenomenon—they are not happening in the air, but only in our brains. Whenever we hear two or more pitches simultaneously, our brains fill in the fundamental of those pitches. If the pitches are tuned in a ratio that corresponds to the harmonic series, the fundamental may be perceived strongly. There are limits to this, e.g., if the ratio is so complex that the fundamental would be below 20 Hz, the bottom of the range of human pitch perception. But again, the violin is in a registral sweet spot where the majority of JI intervals you would want to access in a piece of music can be verified by ear with relative ease.
This is another case where taking a look at the harmonic series makes the concept easier to digest. Below is a series of violin dyads (Fig. 3) that all share a G fundamental. The top staff shows the notes that the violinist plays, and the ratio of the JI interval. The bottom staff shows the fundamental which may be perceived psycho-acoustically when the violinist plays. Refer back to the harmonic series of the violin G string (Fig. 1) and it’s clear that, except for octave transposition, these are the same pitches, the numbers in the ratios corresponding exactly to the partial numbers of the harmonic series. Each of these dyads may be verified by ear by eliminating beats to the greatest extent possible, “locking in” the sonority, and by listening for the fundamental difference tone. There is some precedent for using this phenomenon as a tuning aid: 5-limit difference tones are sometimes referenced in classical violin pedagogy as “Tartini tones,” named for Baroque violinist and composer Giuseppe Tartini. However, I think that violinists would be better served by a holistic pedagogical approach that cross-references the phenomenon of difference tones with study of the natural harmonics of the violin strings.

Fig. 3 – violin dyads from G series
These dyads in Fig. 3 have clear characters (read: timbres) that are strongly identifiable and tied to the prime number family from which they are derived. Ratios of 3 might sound “earthy,” ratios of 5 “sweet,” ratios of 7 “restless,” and ratios of 11 “screamy.” Regardless of the multitude of ornate subjective terms that one might choose to assign, the timbre-characters feel pretty consistent across transposition of pitch and register. A simple transposition from G on violin is to the series of the adjacent string, a D fundamental.
Here is the harmonic series of the violin D string (Fig. 4), and a few violin dyads that all share the D fundamental (Fig. 5).
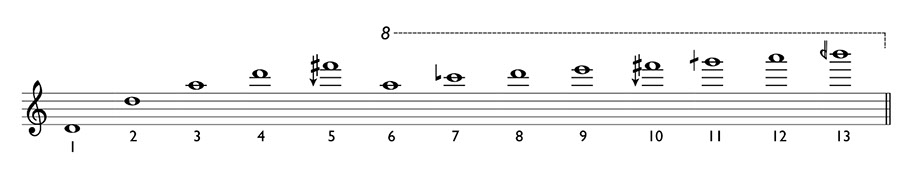
Fig. 4 – D string harmonic series

Fig. 5 – violin dyads from D series
An aside about pitch notation: the practice in use here gives a visual representation of different prime number families and helps signal to the violinist which timbre-character to expect when reading the music. This system is the Extended Helmholtz-Ellis JI Pitch Notation, developed by Marc Sabat and Wolfgang von Schweinitz. It takes Pythagorean as the baseline (i.e., a pitch notated with the traditional natural/flat/sharp symbols would indicate Pythagorean tuning). This makes Helmholtz-Ellis extremely useful for string players by providing a concrete reference point in the Pythagorean-tuned open strings, rather than abstracting from ET.

Fig. 6 – key to Helmholtz-Ellis accidentals (abridged)
III. THE VIOLIN AS TUNER - GRIDS OVERLAID
Fascinating things happen when you begin working with multiple grids of intonation, juxtaposing and intermixing them. For starters, here is a simple dominant-tonic progression in G-Major (Fig. 7). This combines dyads from the D and G spectra from earlier examples. The psycho-acoustic “bassline” matches the function of the harmony exactly. The highest prime used is 7, so this is an example of a passage in 7-limit JI.

Fig. 7 – V-I progression
Here is another example that introduces the IV chord (Fig. 8). Though the presence of a C fundamental adds a bit more complexity, overall this example of 5-limit JI is well within the norms of classical music performance practice.

Fig. 8 – IV-V-I progression
Swapping a V7 chord into the same progression introduces a new element—microtonal drift (Fig. 9). Between the third and fourth sonority something must change in order to keep the dyads in JI. In this solution, as the function of the pitch-class C changes from the root of the IV chord to the seventh of the V7 chord, it drifts down by a septimal comma (about a sixth-tone).

Fig. 9 – septimal drift, downward
Another solution would be to keep the pitch-class C consistent, in which case the F-sharp in the fourth sonority would drift upward by a septimal comma as compared to the F-sharp established by the first sonority (Fig. 10). This solution might be considered more appropriate in a classical music context, since it is common to raise leading tones in classical performance. In practice, a classical musician would likely do some combination of the two, an “intuitive violin temperament” that suggests JI without any extreme shifts in any one voice.

Fig. 10 – septimal drift, upward
Fine negotiations of pitch like this happen all the time in classical ensembles, particularly string quartets, who spend a great deal of time practicing intonation as the blend of the instruments makes tuning discrepancies and beating quite obvious. It is common for a string quartet to operate in a sort of flexible 5-limit JI, shifting individual notes by a syntonic comma here and there as the score demands in order to keep vertical sonorities in tune. And I’ve heard some very special recordings where quartets slide in and out of 7-limit JI, to make dominant seventh chords speak with the utmost power and clarity.
There is an easy rule of thumb for string performance in 5-limit JI: sharps are played a syntonic comma low, and flats are played a syntonic comma high. That way, most notes can be related to an open string in a simple 5-limit ratio, and the instrument retains a ringing quality. For example (Fig. 11), in an A-Major triad, the C-sharp is placed a syntonic comma low so the chord sounds in a pure ratio of 6:5:4. In a B-Minor triad, the root and fifth move down a syntonic comma to keep the minor third in tune with the violin’s D-string, and so the chord sounds in a pure 15:12:10 ratio. Likewise in B-flat Major, you defer to the open D-string by raising the root and fifth of the triad by a syntonic comma, which will sound as a pure 6:5:4. In a string quartet, the tuning of C-Major must always be decided case-by-case, either matching the E-string of the violins or the C-string of the viola and cello.

Fig. 11 – the standard 5-limit tuning strategy: flats high, sharps low
The construction of the violin allows the commas to be studied and practiced with great accuracy. The open strings provide fixed reference points in Pythagorean tuning. You can place a finger on a pitch and verify it against an adjacent open string and keep that finger in position, “saving it” for later, while another finger finds a different pitch and verifies it against a different open string.
The following example (Fig. 12) shows how to accurately find a Pythagorean major third (81:64) and then resolve it by ear to a 5:4 major third. In the first dyad, a 2:1 octave is verified against the open G string with the third finger, which then remains in place. Next, using the first finger, a 4:3 perfect fourth is verified against the open E string and left in place. The resultant dyad on the middle strings is an 81:64 major third. This is easily resolved by ear to 5:4 by sliding the first finger down by a syntonic comma. Practicing this teaches both the sound of the syntonic comma and its feel under the violinist’s fingers.

Fig. 12 – syntonic slide
The next example (Fig. 13) uses a similar procedure to measure the distance of the septimal comma in the violinist’s fingers. The first two dyads are preparatory, to ensure that the high C is tuned Pythagorean. In the third dyad, a 16:9 minor seventh is found by adding a D below the high C (this interval may be verified by ear, and/or checked against the open D string below). Then, slide down to a 7:4 minor seventh by ear.

Fig. 13 – septimal slide
The process of building intervals from open strings while leaving fingers down can reveal many beautiful things. The next example (Fig. 14) shows two procedures for finding the syntonic and septimal commas as dyads. This trains the ear to recognize the difference between two very small yet distinct microtonal beating patterns.

Fig. 14 – two distinct beating patterns
Similar procedures are possible to internalize the sound of the undecimal comma (11-limit) and tridecimal comma (13-limit), and I suppose as many primes higher that one chooses to explore and that the violin’s acoustic properties can accommodate!
Exercises like these form the foundation of practicing advanced intonation on the violin, from reinforcing basics as a student to internalizing the syntonic shifts necessary for a nuanced classical performance to using undecimal relationships to approximate quarter-tones when learning a score in microtonal ET.
To bring these concepts out of the practice room and onto the stage, I’d like to share an excerpt of Eric Wubbels’s “the children of fire come looking for fire” for violin and prepared piano, a duo that Wubbels wrote for us in 2012 that has had a profound impact on my thinking about violin playing and music. This meditative moment from the middle of the 25-minute work uses JI violin dyads to outline a harmonic progression, pulling the listener from simple “major” affect to a complex “minor” one (Fig. 15). The poignant austerity of the moment exposes a psycho-acoustic bassline, which is then reinforced by Wubbels on the piano.

Fig. 15 – “tuning” dyads from Eric Wubbels’s “the children of fire come looking for fire” (2012) for violin and prepared piano
While the introspective nature of the “tuning” section exposes the heart of those dyads, they are deployed throughout “the children of fire…” in various contexts as strongly identifiable timbral entities. Near the conclusion of the piece, the fire is unleashed:
IV. NEXUS OF PITCH-CLASS
After exposing the ear to microtones for even a short time, semitones start to sound enormous in breadth. Likewise, as a violinist, after growing accustomed to gradations of pitch as small as the syntonic comma, the distances between semitones under the fingers begin to feel like vast expanses. For a violinist playing music that is limited to the 12 chromatic pitch classes, in the absence of keyboard or another fixed-pitch instrument, the target area for any given pitch is actually quite wide and vaguely defined.
I prefer to have well-marked trails to travel along my fingerboard, and as many resources as possible in my creative toolbelt. Far from limiting spontaneity in a performance, a precise catalog of microtonal inflections for each pitch-class allows the violinist to deploy just the right shading in performance, or to make a choice that is perfect in the way that it is “wrong.” It’s difficult to be truly adventurous if you don’t know which path you’re straying from.
Let’s take a look at five inflections of the pitch-class C, organized from lower to higher. First, here they are in the context in which they might typically be found in a classical or contemporary work (Fig. 16).

Fig. 16 – inflections in context
The first one, C lowered by a septimal comma, is part of a just-intoned dominant seventh chord, as might be employed by a string quartet, a brass choir, or in solo Bach; next, the C is lowered by a syntonic comma in order to sound in tune as part of an A-flat Major chord; then, C Pythagorean is employed to match the violin’s G-string, or perhaps to approximate ET; C is raised by a syntonic comma to match the violin’s open A and E strings in an A-Minor chord; Finally, C is raised by an undecimal comma to sit in a spectral sonority on a G fundamental, or alternately as an approximation of an ET quarter-tone.
In isolation, any of these versions of C may be verified by eliminating beats (or, in the case of septimal and undecimal sonorities, memorizing the “locked in” beating pattern) and listening for the psycho-acoustic fundamental (Fig. 17).

Fig. 17 – inflections isolated as verifiable JI violin dyads
The first one, C lowered by a septimal comma, is part of a just-intoned dominant seventh chord, as might be employed by a string quartet, a brass choir, or in solo Bach; next, the C is lowered by a syntonic comma in order to sound in tune as part of an A-flat Major chord; then, C Pythagorean is employed to match the violin’s G-string, or perhaps to approximate ET; C is raised by a syntonic comma to match the violin’s open A and E strings in an A-Minor chord; Finally, C is raised by an undecimal comma to sit in a spectral sonority on a G fundamental, or alternately as an approximation of an ET quarter-tone.
In isolation, any of these versions of C may be verified by eliminating beats (or, in the case of septimal and undecimal sonorities, memorizing the “locked in” beating pattern) and listening for the psycho-acoustic fundamental (Fig. 17).

Fig. 18 – inflections as musical resources
These inflections appear all over Western music and are innately familiar in a violinist’s fingers—the challenge is in knowing that the inflections are there and that they exist at distinct, verifiable points, a nexus around each pitch-class formed by overlapping grids of tuning. Beyond a harmonic, JI usage, the commas may be used to approximate ET microtones (syntonic = ca. eighth-tone; septimal = ca. sixth-tone; undecimal = ca. quarter-tone). The daunting proposition of learning a microtonal language in the abstract, or by watching the dial of a digital tuner, is rendered moot—all the tools necessary are under the violinist’s hands and within their mind.
PART TWO: ZONES OF LIGHT AND DARK
I. THE PULL TOWARD BACH
It was around the 2011–12 concert season that JI burst into the forefront of my consciousness. I had gotten my feet wet performing JI-infused works by Taylor Brook (Vocalise), Chiyoko Szlavnics (Triptych for AS), Mario Diaz de Leon (Trembling Time II), and Sam Pluta (Broken Symmetries), and was in the midst of two long-term duo projects with Kate Soper and Eric Wubbels that fueled our mutual interest in JI. Both Soper’s work, Cipher, and Wubbels’s work, “the children of fire come looking for fire”, involved serious investigations into how to produce and control pyscho-acoustic difference tones as a creative tool. We met up every week or so to try out material, and the pieces developed organically from the collaborative process. It was a beautiful way to work, especially in a premiere-fueled contemporary music economy that tends to prioritize efficiency over personal relationships.
Gaining access to the bass register as a violinist, being able to create and manipulate a psycho-acoustic “bassline” using the violin alone, was a huge revelation. I started to work on playing techniques to make the difference tones more palpable. Playing with a bright (i.e., overtone-rich) sound helps—the additional upper spectra reinforce the fundamental more strongly. The sound also needs to be as consistent as possible because even tiny changes in bow pressure will change the pitch and disturb the difference tone. The difference tones are optimized by a firm, slow pull of the bow with consistent pressure throughout the stroke.
Beyond the intriguing prospect of sustaining three-part harmony on the violin, the varied timbral effects of dyads based in different primes are wonderful. First of all, the notes of the dyad and the difference tone sit together in a spectrum, giving the impression of a single fused entity rather than multiple pitches, creating a balanced sonority while maximizing the resonance of the violin. This fusion of pitch simultaneously manifests as timbre, the sound of the instrument morphing as sonorities change from, say, the sweet tranquility of a syntonic (5-limit) harmony to the dark urgency of a septimal (7-limit) harmony’s “locked in” beating pattern. These shifts from one prime to another can be deeply affecting on an emotional level. These elements—harmony, fusion/balance, timbre, emotion—are each powerful creative tools and are all connected and unified by the properties of prime number families.
The thought of these sort of celestial elements of music-making being unified by the primes seems very Bach-like. J.S. Bach’s music is hyper-organized, balanced, laced through with numerological symbols, yet capable of conveying incredible emotion and seemingly communicating from a higher, spiritual plane. The Six Sonatas and Partitas for Violin Without Bass Accompaniment (1720) stand as towering examples of the violin’s potential. Lost for a time and then relegated to the status of etudes, the Sonatas and Partitas have, since the 19th century revival of Bach’s music, come to be regarded as the highest peak of violin performance, the ultimate test of a violinist’s technical skill and musical maturity. Paganini is for hotshot kids. Bach is forever.
Part of the mystique of the Sonatas and Partitas is in their infinite potential for reinterpretation. This is densely polyphonic music, usually composed in three- or four-voiced harmony, yet the construction of the violin allows only two pitches to be sustained simultaneously. In practice, these works represent a brilliantly executed illusion of polyphony. Riddled with intriguing omissions, the Sonatas and Partitas are beautifully ambiguous in their harmonic design. In the hands of expert violinists, there are seemingly endless interpretations that each seem perfect in their own way. Furthering the mythos is research that suggests that Bach wrote the Sonatas and Partitas, and particularly the emotionally devastating Ciaccona, from the D-Minor Partita, in response to the death of his first wife, Maria Barbara Bach. German musicologist and violinist Helga Thoene uncovered a series of “hidden chorales” and numerological codes encrypted within the Ciaccona. The chorales, short excerpts of Bach’s previous work, are fixated on death. This interpretation was realized by violinist Christoph Poppen and the Hilliard Ensemble on the unexpectedly popular 2001 album Morimur (ECM Records). Though the veracity of Thoene’s findings are disputed in musicological circles, as an artistic interpretation the results are absolutely gorgeous.
My work with JI in a contemporary music context and my fascination with the Morimur album provided the spark that began my own journey with Bach’s solo violin music. Could a “hidden counterpoint” of difference tones be revealed by performing Bach in JI? And what other expressive avenues might that open up? Any modern interpretation of antique music is contemporary by its nature. What kinds of details long obscured might be illuminated by embracing a contemporary approach to violin sound?
II. HARMONY: HIDDEN COUNTERPOINT / WIDENING THE CONSONANCE-DISSONANCE CONTINUUM
The opening sonority of the Adagio from Sonata No. 1 in G-Minor is iconic. A root position G-Minor chord in harmonic voicing spanning all four strings of the violin, it sets the tone for the entire cycle of Sonatas and Partitas—dark, open, and resonant. And it immediately presents the intonation-minded violinist with an intriguing decision.
Regardless of the tuning choice that one makes, minor chords are inherently in conflict with themselves—the root of the chord in terms of functional harmony will always be at odds with the fundamental implied by the sonority. The common 15:12:10 tuning of a minor triad sounds “normal” to Western ears (the tuning most commonly employed by string quartets, e.g.), but the acoustic fundamental is a major-third lower than the functional tonic (Fig. 19). The less common 9:7:6 minor triad is similarly conflicted—the acoustic fundamental is a perfect-fifth lower than the functional tonic (Fig. 19).

Fig. 19 – the inner conflict of minor triads
This internal struggle is responsible, at least in part, for the “sad” affect of minor keys. Another option would be to tune minor-thirds Pythagorean (32:27), which offers a compromise somewhat akin to ET, but, still, does not resolve the conflict.
An added dimension for violinists is the manner of breaking the chords, since the violin is only capable of sustaining two pitches simultaneously. All of these factors add up to a wide open field of interpretive choice—there is no “right” answer.
To perform the opening chord of the Adagio in 7-limit JI, there are no fewer than four options (Fig. 20).

Fig. 20 – G-Minor Adagio opening sonority: four options
The ratios here refer to the pitches that are being sustained after breaking the chord. The first choice, 5:3, is the most standard, and the most bright. The second choice, a Pythagorean major sixth (27:16), also falls within the norms of standard performance practice, but is less resonant because the sustained pitches are in such a complex relationship as compared to the simple 5:3. The third, 12:7, is unorthodox, powerful, and intriguing. The fourth option, 8:3, is also unorthodox, but for different reasons.
I consider all four of these sonorities to be beautiful. But I find the fourth option, 8:3, to be the most convincing statement as the opening of a JI interpretation of the Bach cycle. By breaking the chord in unusual fashion, the G and D are sustained in an 8:3 ratio, producing a G fundamental. Despite the minor key, the “G-ness” of the opening is reinforced. It simultaneously grounds the harmony while saying “this isn’t your grandparents’ Bach interpretation.”
As the opening phrase continues, performance in 7-limit JI yields purely tuned and maximally resonant dominant seventh sonorities that reinforce the functional harmony, while microtonal inflections carried through the measures vivify the fast ornamental lines that rebound from arrival points (Fig. 21).

Fig. 21 – opening phrase of the G-Minor Adagio in 7-limit JI
In the opening of the Adagio, performance in 7-limit JI anchors the passage, and as the movement progresses, JI tunings at arrival points sketch out a psycho-acoustic bassline that alternately may reinforce the implied harmony or subvert it. In other cases, tuning choices may be used to heighten the feeling of tension and release through a musical phrase, as in this sequence of suspensions from the C-Major Largo (Fig. 22).

Fig. 22 – C-Major Largo, suspensions
In this section of the Largo, playing the V7 chords in a pure, septimal tuning results in heartrendingly dissonant fourths (21:16) on strong beats as the seventh becomes part of a 4-3 suspension, which then resolves. This phrase is played again a whole-step higher with the same tuning scheme, ratcheting up the tension as the register rises. There are a few key things that this treatment of the passage highlights. First, it embraces the idea from Baroque music theory that the interval of the fourth is a dissonance. It also greatly expands the expressive range of the music as compared to standard performance practice (in which those fourths would be tuned as 4:3 perfect fourths) by introducing extreme beating on one end of the spectrum as a counterbalance to a pure, beatless sound for points of resolution, thereby granting access to a wide field of subtleties in between. And finally, the inner life of the beating intervals infuses them with a propulsive quality that builds momentum as the phrase develops, launching the violinist organically into the following, climactic passage. This can be felt as the instrument vibrates in your hands; it’s like a form of haptic feedback where the buzzing of harmonic/acoustic complexity physically agitates your fingers into action. As a player, it’s as if these creative and calculated tuning decisions take some of the onus off of you in performance to muscle through a phrase and “make something” of it; rather than clawing up a difficult precipice, you are surfing atop a great wave.
III. CIACCONA: TIMBRE, RESONANCE, SPIRIT
If the Sonatas and Partitas are the tallest mountain in the violin literature, the Ciaccona is the summit. At about 14-minutes it is remarkably long for a Baroque movement and represents the emotional center of the entire cycle of works. The Ciaccona is constructed as a set of continuous variations over a four-measure repeating bassline and is structured in three large sections: D-Minor/D-Major/D-Minor. It is widely considered one of the greatest works in the Western musical canon, all the more extraordinary as it is composed within the austere confines of a lone soprano instrument.
As a violinist setting out to interpret the Ciaccona, the weight of the piece is almost too much to bear. The technical challenges of playing the work and its musico-spiritual transcendence would be enough to make one feel small, but then there are the traditions and practices lodged in the music from centuries of performance and teaching, the magnetic pull of past interpretations, the sense that there is a “right” and a “wrong” way to perform the piece. It can be difficult to lay these concerns aside, to weed out and untangle precedents from the music itself, to seek out what one really wants to say with this music as a performer. After turning my back on the piece for some years, JI and contemporary performance practice brought me back to it. I finally felt like I had something to say with the Ciaccona that was worth sharing, that would perhaps illuminate some shadowy corners of the music that hadn’t yet been encountered.
The famous opening triad of the Ciaccona is in a dark, throaty register of the violin in a closed voicing. As a minor chord, it carries the same internal conflict that makes the intonation of the G-Minor Adagio such an interesting question. A standard classical performance practice, in which flats are generally played a syntonic comma high and sharps a syntonic comma low, keeps tuning pretty consistent within pitch-classes, with small adjustments required occasionally as phrases modulate from one key area to another. A standard tuning of the opening phrase of the Ciaccona might look like this (Fig. 23), or be played in an “intuitive violin temperament” that approximates the same idea.

Fig. 23 – Ciaccona, standard interpretation
This tuning works well, but to my ear it doesn’t match the character of the opening. In theory, the first sonority tuned 15:12:10 aligns all three pitches atop the same fundamental, B-flat. However in practice, the violin sustains only the top two pitches, which reduce to a 5:4 ratio, a registrally bright major third with an F fundamental.
On the other hand, the tuning 9:7:6 includes a prime and is therefore irreducible, so regardless of the way a violinist breaks and sustains the chord, the sonority is locked in a single harmonic spectrum, each pitch reinforcing the others. The 9:7:6 tuning of the opening triad of the Ciaccona establishes it as a sound-object with a distinctly dark, buzzing septimal character, and carries implications for the rest of the opening phrase (Fig. 24).

Fig. 24 – Ciaccona, interpretation in 7-limit JI
Just as the introduction of beating fourths in the C-Major Largo widened the range between most-dissonant and most-consonant, beginning the Ciaccona with the septimal minor triad opens up fissures that radiate throughout the piece and expand the violinist’s expressive resources. This operates on a few levels. The 9:7:6 D-minor triad is enmeshed in a web of expectations. Acoustically, it is strongly rooted in a G fundamental by its relatively low position in the harmonic series, possessing an inherent quality of solidity and “home” with a simultaneously unsettled character, a drive to “resolve,” brought on by the septimal beating pattern. This agitated character is further complicated by the conflict between the psycho-acoustic presence of G and the acoustic primacy of the D tonic, and complicated further still by our cultural expectations of what a D-Minor triad “should” sound like and our memory of how the opening of this revered piece of music is usually performed.
Between all of those characteristics and implications—acoustic, psycho-acoustic, cultural— the 9:7:6 is one hell of a sound object. These are all factors that make it strongly identifiable, standing in sharp relief to syntonic and Pythagorean sonorities, enabling tectonic shifts between distinct timbre-characters from phrase to phrase. It also means that there are many inflections to work with for any given pitch-class.
In the G-Minor Adagio, my goal was to reinforce the harmony implied by the notation, an analytical process. In the Ciaccona, the approach was much more intuitive, oriented towards timbre and heightening the expressivity of phrase shapes. For example, I’ve always regarded the third measure of the Ciaccona as a glimmer of optimism as the harmony changes to B-flat Major (see Fig. 24). 7-limit JI allows the distance to be dramatically widened between the darkness of D Minor and the brightness of B-flat Major. First of all, the affect of those key areas is made markedly different by the contrasting use of septimal and syntonic harmony. Furthermore, the pitch-class F in m. 1 is inflected downward by a septimal comma, while the same pitch-class in m. 3 is shaded upward by a syntonic comma, resulting in a span of nearly a quarter-tone between those two versions of F. What started as a musical idea of darkness and light is made manifest acoustically as a microtonal change in register within a single pitch-class.
Just like in the C-Major Largo, the availability of all of these subtle gradations of pitch allow dissonances to take on a gut-wrenching intensity, as in the first beat of m. 2 of the Ciaccona (Fig. 24). The G is lowered by a septimal comma, anticipating the purely tuned A7 chord on the next beat. Consequently, the D and G on beat 1 form a brutal 21:16 fourth, which is made even more dissonant by the upper notes of the chord. Thus, the resolution to a perfectly tuned A7 chord on the next beat becomes an oasis of repose, not only heightening the ebb and flow of harmonic tension, but also highlighting the feel of the sarabanda dance rhythm in which the Ciaccona is based, a three-beat pattern with special emphasis on the second beat.
The return of septimal tuning in m. 4 introduces a new element. As before, the septimal intonation of minor sonorities means that all notes in the chord are in the same harmonic series, so the resonance of the violin is maximized. But now, the microtonal inflections also enhance the effect of a lamento descending motif that is pervasive throughout the Ciaccona. Coming from the optimistic brightness of the syntonic B-flat in m. 3, the septimally lowered B-flat in the soprano line in m. 4 is jarring. In terms of melodic contour, all of the septimally inflected notes in m. 4 drive the line inexorably lower, culminating in another anguished 21:16 fourth on the downbeat of m. 5.
Opportunities to shape the music through this minute attention to detail abound throughout the Ciaccona and form the building blocks of “zones of light and dark” that operate on every level of the piece, portrayed in vivid color through JI. From beat to beat, dissonance and resolution take on wrenching immediacy. From phrase to phrase, tectonic shifts between JI timbre-characters lift up plateaus of optimism and carve out valleys of introspection and gloom. This motion is reflected on a formal level as the piece moves from D-Minor to D-Major and then back to D-Minor. And on a meta level, the entire D-Minor Partita connects to the C-Major Sonata as a diptych, an overarching journey from darkness to light, from death to resurrection.
There is a popular idea that once a musician has developed a critical level of skill, and become a “virtuoso,” performing music is easy, and this feeling of ease qualifies a performance as great. This is an illusion. For a great performance to happen, a musician must strive to inhabit an elevated plane, a space above the heads of performer and audience where sound and consciousness intermix. The journey to this high country is difficult, and becomes ever more demanding the higher one ascends. Akin to practices like yoga and meditation that help people achieve clarity in their daily lives, the technical and intellectual tools of a violinist blaze the paths to the upper reaches. When you stumble, you won’t fall too far. When you veer onto unexplored spurs, you are not lost.
The structure woven by the study of intonation systems is a great asset for string players, and the acoustic properties of JI that manifest not only as pitch but also harmony, timbre, and emotional expression make it a tool that enriches many facets of music. For me, JI has become a critical component in a holistic approach to sound, one part of a performance practice forged in the NYC contemporary music community that resonates equally in collaborations with composers on notated scores, as part of an improvised language, and in the music of J.S. Bach.
To the wild places of sound and thought, let us travel. My bags are packed.

Josh Modney is violinist and Executive Director of the Wet Ink Ensemble and a member of the International Contemporary Ensemble (ICE), and performed with the Mivos Quartet for eight years, a vital new-music string quartet he co-founded in 2008. Modney’s fresh and versatile approach to the violin and uniquely dynamic performance practice has made him a highly sought-after collaborator. He has worked closely on new solos and duos with composers including Kate Soper, Alex Mincek, Eric Wubbels, Sam Pluta, Andrew Greenwald and Rick Burkhardt, as well as projects with major figures including Kaija Saariaho, Mathias Spahlinger, Helmut Lachenmann, George Lewis, Christian Wolff, and Peter Ablinger.
Photo by Alexanader Perrelli
